Ah, the Square Wave. You know it, you love it. So simple, yet so complex. Almost every oscillator in electronic music offers a Square Wave output. It's the waveform you turn to for all odd harmonics and no even harmonics. It has a distinctly hollow sound; the sound of a clarinet or a closed-end organ pipe.
Some would argue that the Square Wave does not exist in nature. My fuzzbox might disagree. But nonetheless, it is difficult to find mechanisms in nature that approach the instantaneous transitions of a perfect Square Wave, or to find mechanisms that have a Square Wave as their core operation.
The square wave is easy to make, electrically. It just slams between two values. It's binary. And that has some implementation advantages. Inexpensive digital circuitry can be used to create the waveforms. And a single Exclusive-OR gate will perform Ring Modulation on Square Waves, as implemented on the ARP Odyssey.
Toggle flip flops naturally produce square waves an octave below their input frequency. Of course. And we use those in many ways in electronic music:
And the specialized Buchla 144 Dual Square Wave Oscillator even goes to the trouble of having the core VCO drive a toggle flip flop to guarantee that there is no second harmonic.
The square wave has the lowest Peak to RMS voltage ratio possible, as the peak level of the square wave is the RMS level. Nonlinearities do not affect the mighty square wave.
The binary nature of the square wave is also problematic in that it covers up organic subtleties. Examples would include Phase Modulation and Frequency Modulation. There is a threshold of sensitivity below which modulation has no effect on a square wave. The highest threshold is at the center of the flat area and the lowest threshold is at the transitions. Once that line is crossed, the square wave reacts suddenly.
So here is a plot of the classic square wave.
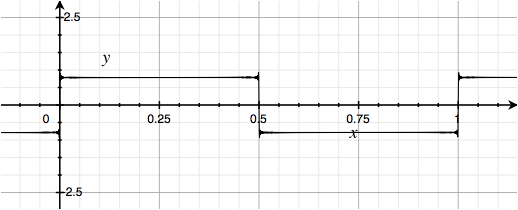
The equation is:
Where is the frequency in Radians/Second.
(This and the other plots were drawn in Apple's Grapher application from hundreds of sines and cosines. There are some visible artifacts. To make the presentation clearer, the axis in the plots is scaled to be the same as the value in the equations with .)
The contribution of each harmonic is inversely proportional to its frequency in what is called a Harmonic Series. Since only odd harmonics are present, this specific situation is called an Odd Harmonic Series.
We can show how the square wave is built up from component Sine Waves at odd harmonics:
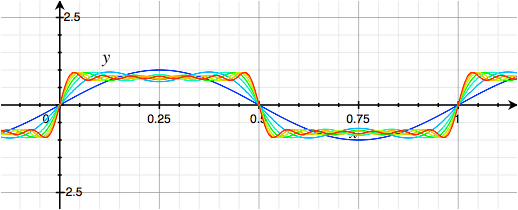
The zero-crossing transitions at 0 and 180 degrees are all lined up, so the sum of an infinite number of slopes creates instantaneous transitions. And in the flat sections, the ripples of each successive odd harmonic show up in alternate polarities and quickly converge to a constant level of . This is related to the Leibniz Forumla for π.
So the first question is, what happens if we sum Cosine Waves instead of Sine Waves. The result is completely different:
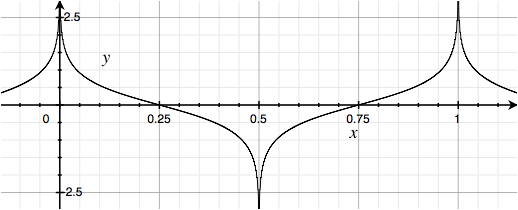
Isn't it amazing what a phase shift can do? This waveform shares none of the graphical aspects of the original Square Wave. The binary nature has completely vanished. In fact it's the opposite, with points instead of flats. Yet the harmonic power spectrum is identical; there is exactly the same amount of each harmonic as the original Square Wave.
I've heard this called a Hilbert Wave. A Hilbert Transform rotates the phases of a given signal 90 degrees, and the classic example of its effect is to plug in a Square Wave.
Here is the build-up of that from component Cosine Waves:
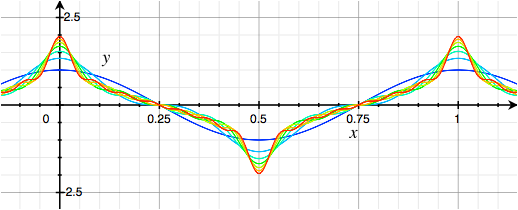
And sure enough, the humps of all the component waves are now adding up to create peaks, and in between the ripples of the component waves cancel out to a smooth slope.
The peaks of the Hilbert Wave are theoretically infinite, but the Harmonic Series goes up so, so, slowly that the first 500 harmonics bring it up to only 3.75 (with respect to the 1.0 fundamental). So in practice, it's a far cry from infinity.
So we've tried summing sines and summing cosines. How about rotating between , , , and over every four harmonics? What would that look like? Here:
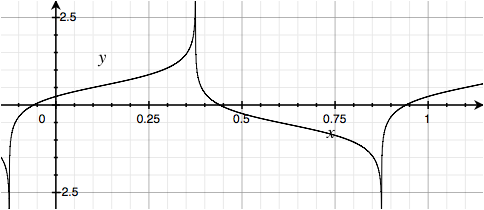
That wave is graphically somewhere in between the two previous waveforms, which is interesting because the Square Wave and Hilbert Wave are so different.
And left-right symmetry is gone, the longer near-vertical transistion is on the trailing edge, so one can discern positive vs. negative frequency.
And by playing with the phases it is possible to morph from Square Wave to Hilbert Wave like this:
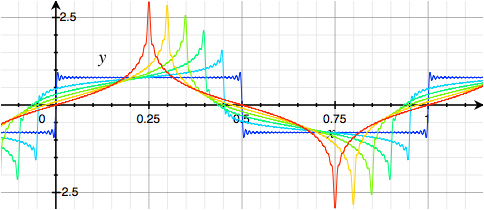
(This is with the phase of the fundamental held constant at 0 degrees.)
Here's another variation; instead of rotating between the four quadrature phases, how about just alternating between sines and cosines? Here:
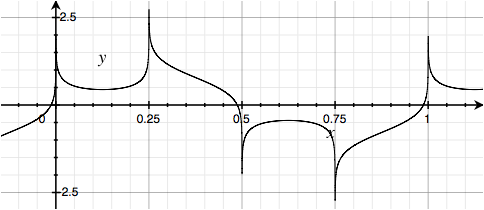
Weirder still, pairs of sines alternating with pairs of cosines:
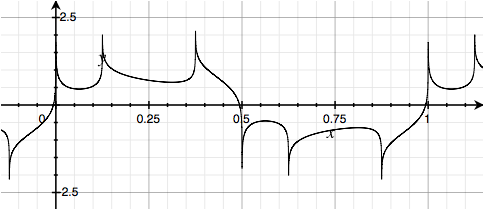
Here are all sines, but invert the polarity of the last of each group of four harmonics:
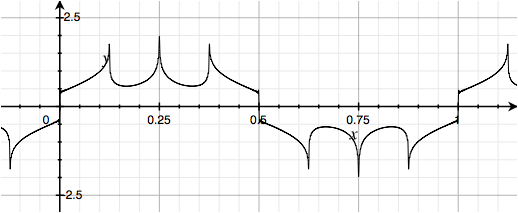
All sines, but invert the polarity of the third of each group of four harmonics:
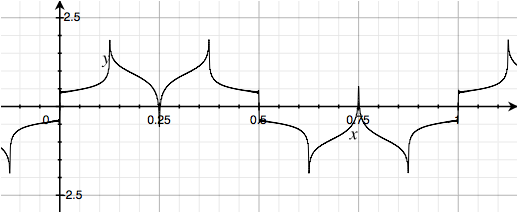
All sines, but invert the polarity of the second of each group of four harmonics:
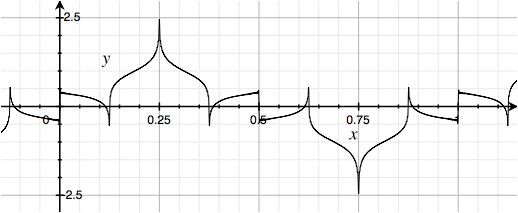
And all sines, but invert the polarity of the second, third and fourth of each group of four harmonics, effectively inverting the polarity of the first:
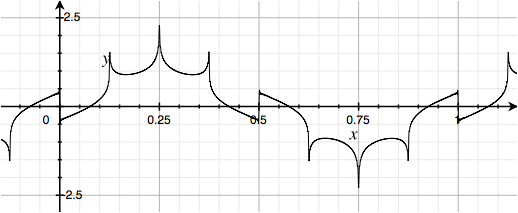
Now, if we group the harmonics into threes instead of fours, we can replace the middle of each trio of harmonics with a Cosine:
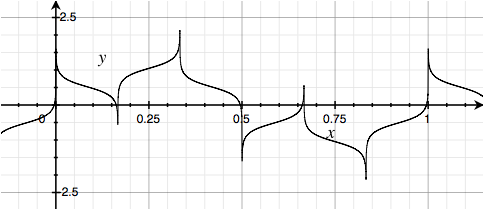
Or replace the third of each trio of harmonics with a Cosine:
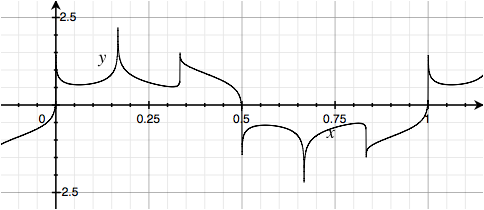
Again, all of these have the same power spectrum as the classic Square Wave.
Well, those are all graphically pretty far removed from Square Waves. Is it even possible for polarity or phase variations that are recognizably related to Square Waves? Yes, if one inverts the polarity of symmetrically located coefficents within equal groups of harmonics.
For example, if you take the Square Wave spectrum and invert the phase of the middle two of every group of four harmonics, you get this:

That's very much like a Square Wave. Let's call this a Tri State Square Wave.
A variation of this, inverting the last two of each set of four harmonics, generates what I would have to call a Tri State Hilbert Wave:
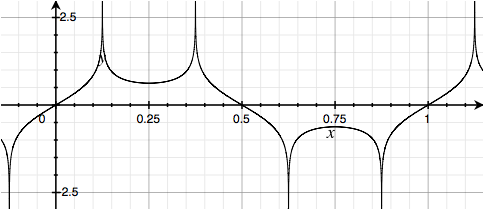
But back to the squares...
In a similar way, if we invert the middle of each group of three harmonics, we get a stairstep version of a Square Wave:
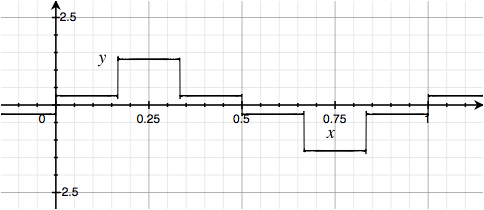
Similarly, we can do groups of five harmonics at a time and invert the middle one:
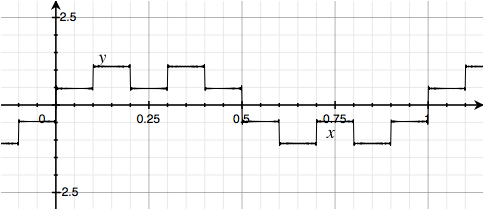
Or invert the two near-middle harmonics in each group of five:
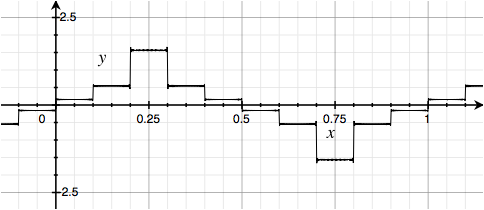
Or invert the three middle harmonics in each group of five:
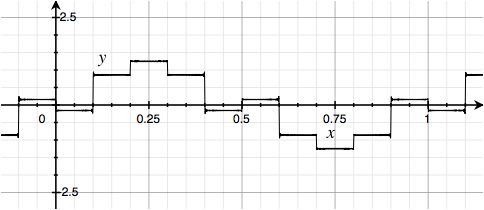
And finally, here is a waveform with the spectrum of a Square Wave, but the phases are random:
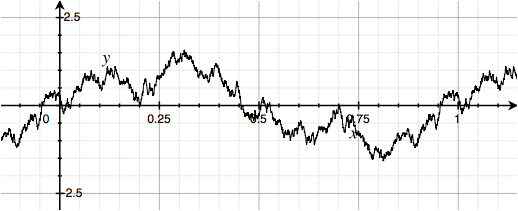
All of the waveforms presented here have the identical power spectrum, the same contribution of each harmonic. Only the phases or polarities have changed. Will they sound identical? Yes, at least to a first approximation.
The ear is not very sensitive to phase, but there are experimental situations where it can be. Nonlinearities will affect the waveforms in different ways, and there are nonlearities all around; in circuitry, in speakers or headphones, in the air, and in our ears. And in any kind of real world application, a lot happens after the waveform is first created.
I just think it's interesting, that's all.
Donald Tillman: Synth-DIY -- Buchla 144 Dual Square Wave Oscillator
Series Math Study: A Brief Note on Nth Partial Sum of Harmonic Series
Bernard Hutchings, Jr.: Experimental Electronic Music Devices Employing Walsh Functions
Wikipedia: Apple Grapher
Wikipedia: Harmonic Series
Wikipedia: Hilbert Transform
November 4, 2013: Fixed a unit, added the random phase wave.